大学受験の数学対策として、問題集にくり返し取り組んできた人がほとんどでしょう。そのため、

と考える人がいるかもしれません。
しかし、実はそれは違います!

数学の勉強は、過去問演習までしっかり取り組むことで完成します。過去問演習に取り組むことで、自分の志望校の出題傾向を掴み、効率的に苦手分野を克服できるようになるでしょう。
とはいえ、
- 具体的にどうやって過去問演習すれば良いの?
- そもそもイマイチ過去問演習の重要性がわからない!
という人も多いはず。
今回の記事では、そのような人に向けて過去問演習が大事な理由や、具体的な勉強方法などについて解説します!過去問演習で受験生が抱えがちな疑問点についても解説しているので、ぜひ最後まで読んで参考にしてみてください。
過去問演習が大学受験の対策に必須な理由は?
過去問演習をはじめるまでに、多くの人が「問題演習」を積み重ねてきたと思います。
しかし、油断は禁物です。過去問演習をせずに問題演習までで勉強を終わらせてしまうと、志望校合格に必要な実力は身に付きません。
なぜ、問題演習で終わらせてしまうと、志望校合格に必要な実力が身につかないのでしょうか?それは問題演習と過去問演習は役割が違うからです。
問題演習と過去問演習は、以下のような違いがあります。
- 問題演習:全単元・全種類の問題を解けるようになるために行う
- 過去問演習:問題演習で積み上げた知識を入試で活かせるようにするために行う
過去問演習には「現在の実力を測る」という目的もありますが、それ以上に「問題演習で積み上げた知識を入試で活かせる状態にする」という役割が大きいです。
問題集では「この章で2次関数を勉強して、こっちの章ではベクトルを勉強して・・・」というように、単元ごとで集中的に勉強することが多いです。こうした幅広い単元を集中的に解くことで、入試で求められる実力の基礎を身につけられるわけですね。
一方で過去問演習の場合は、問題集で身につけた知識を「各大学の出題傾向に合わせて引き出せるように取り組む」ことが大切です。問題集と違って「出題単元がランダム」「出題されやすい問題など一定の傾向がある」などの特徴が過去問にはあるので、これに合わせて力を発揮できるようになる必要があります。
どれだけ問題演習で数学の知識を身につけても、入試本番でその知識を柔軟に引き出せなければ意味がありません。
特に入試本番では制限時間があるため、普段の問題演習と同じ感覚で解いていると「焦って間に合わない」ということもあり得ます。


「ランダムな出題で解く」「大学の傾向に合わせた問題を解く」「制限時間内に解く」という経験は、過去問演習でなければ積めません。さらに過去問演習に取り組むことで、「答案の書き方」「1問あたりにかけられる時間の長さ」などを実際に経験できるのです。
過去問演習で実力を発揮できるようになるためには、以下の2つを意識しましょう。
- 過去問を使って時間配分を意識する
- 解いた過去問を復習して頻出分野や苦手分野を克服する
過去問を使って時間配分を意識する
過去問に取り組む際は必ず時間配分を意識しましょう。
問題演習に取り組む際は、そこまで厳密に時間を気にしている人は少ないのではないでしょうか?わからない問題があれば、じっくり時間を使って考えることが多かったはずです。
しかし、入試本番では制限時間があるため、問題演習のように「じっくり考える」ということはできません。
入試で満点を取る必要はありませんが、確実に取れる問題を時間内に解いて、目標点数を超えるには、実際の入試を意識した時間配分が重要になります。また、「わからない問題を飛ばして確実に取れる部分で点数を稼ぐ」という判断ができるようになることも必要です。
こうした「わからない問題を飛ばして取れるところを確実に取る」という練習は、過去問演習でなければできません。

そう思う人がいるかもしれません。
しかし、過去問では正答率を計算できるので、問題演習とは緊張感が全く違います。問題集なら何問飛ばしても気楽に進められますが、過去問では「こんなに飛ばしたら受からない」という具体的なイメージを持ちつつ勉強することができるからです。
さらに難関大であれば、解答だけでなく「答えに至る経緯」を記述させることが多いです。この場合、解答が合っていても「答えに至る経緯」が間違っていると減点されます。証明や図示をしなければいけない問題もあるでしょう。
一方で、答えが出なくても、途中式で解答の方針を示すことができれば部分点をもらえるケースがあります。

このように、「取れる問題で確実に満点を狙う練習」「最後まで解けなくても部分点を狙う練習」などを過去問演習で行いましょう。
また、時間配分を考えるうえではマーク式の訓練も必要です。

いいえ、解答形式がマーク式でも油断はできません。マーク式はキレイに塗り潰さないと読み取ってもらえないため、意外と時間がかかります。
また、マークする問題番号がズレていないかの見直しも必要ですし、マークがズレていたら修正する時間も必要です。マークが1つズレただけで、すべての解答がズレて0点になることもあり得ます。
実際の入試では、緊張なども影響して上記のようなマークミスが起こりがちです。そうしたミスを防ぐためにも、過去問演習で入試を想定して問題に取り組み、余裕を持った時間配分を考えましょう。
解いた過去問を復習して頻出分野や苦手分野を克服する
過去問を解いたら必ず復習して、頻出分野の確認や苦手ジャンルの克服を行いましょう。
過去問を解くことで、大学ごとの頻出分野を把握できます。例えば早稲田大学の商学部の場合、2016〜2020年の傾向を見ると、以下の5分野が頻出であるとわかります。
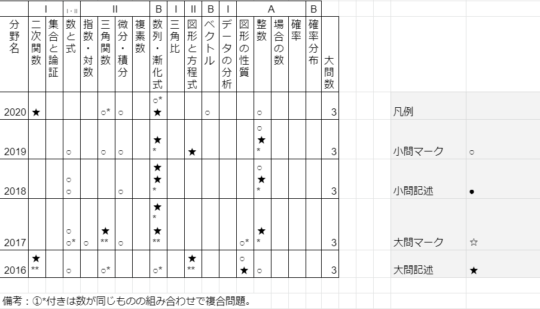
- 数と式
- 整数
- 微分積分
- 三角関数
- 数列・漸化式
一方で一橋大学の数学では、以下の分野が頻出です。
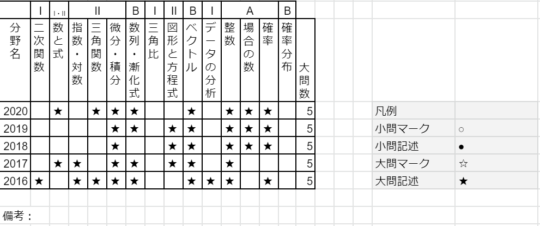
- 微分積分
- ベクトル
- 整数
- 数列・漸化式
- 確率

こうした頻出分野は、自分が受験する年度の入試でも出題される可能性が高いです。そのため、出題傾向を把握して頻出分野の大問だけでも確実に得点できれば、合格最低ラインをクリアできる可能性が高くなります。
もし「頻出分野の中に苦手ジャンルがある」という場合は、重点的に克服しましょう。頻出分野内に苦手な内容があると、せっかく出題範囲を予想できても得点を逃すことになりかねません。

このように思う人もいるでしょう。
しかし問題演習の場合は、単元別に順序よく問題が掲載されており解説もまとめられているため、自然と正答率は上がります。
一方の過去問では単元がシャッフルされて出題されるため、

となりがちです。入試本番でこのような状況になることは避けたいですよね。
入試本番に近い状態で問題に取り組んだうえで「自分はどこが苦手なのか」を正しく把握し、確実に克服しましょう。

数学の過去問演習の勉強手順
最後に過去問演習の手順について解説します!数学の過去問演習は、具体的に以下の手順で進めましょう。
- ステップ1
- 解答用紙を準備する
- ステップ2
- 時間を計って解く
- ステップ3
- 解説を全て読む
- ステップ4
- 得点を記録する
- ステップ5
- 間違えた問題を解説を閉じて解きなおす
- ステップ6
- 苦手分野が見つかったら問題集で苦手を克服する
ステップ1.解答用紙を準備する
まずは解答用紙を準備しましょう。解答用紙は、志望校の本番と同じ大きさのものを準備することが理想です。有名な大学であれば、Webで検索すると解答用紙が見つかります。共通テストであれば、赤本などに付属されているものを活用しましょう。
ただし全ての大学で解答用紙が見つかるわけではないので、見つかった場合のみで大丈夫です。

いいえ、実は違います!入試本番に近い紙を使って演習することで、書ける文字の大きさや記述量、計算に使える余白の大きさなどを正確に把握できます。本番で「余白が意外となくて途中式を全部書けない・・・」とならないよう、できれば志望校と同じ紙を準備しましょう。
ステップ2.時間を計って解く
紙を用意したら、実際に時間を計って解きましょう。
入試には制限時間があるため、「1問1問じっくり時間をかけて解く」ということができません。難しそうな問題はサクッと飛ばして、確実に取れる問題を解くことが重要です。そのためにも、入試本番と同じように時間を測って、受験当日をイメージしながら解きましょう。
また、問題を解くだけでなく「テスト終了前の見直し」の時間も考慮が必要です。見直しの時間まで意識しておけば、入試本番で「計算ミスに気づいた」「マークズレが起きた」という場合も、余裕を持って対処できます。
ステップ3.解説を全て読む
問題を解き終えて丸付けをしたら、正解・不正解にかかわらず、全ての問題の解説に目を通しましょう。
不正解の問題については、解説を読んで「なぜ間違えたのか」という理由を把握しておきます。正解した問題であっても「考え方が違った」「もっと効率的な解き方があった」という発見があるかもしれません。
もしかすると、たまたま正解していただけのこともあるでしょう。たまたま正解していた問題を、

と放置すると、入試で似た問題が出題されたときに対応できません。
間違えた問題はもちろん、正解した問題の解説までしっかり読み込み、本番で対応できるようにしておきましょう。
ステップ4.得点を記録する
解説を読んだら、採点して自分の得点を記録しましょう。
とはいえ、厳密に得点を記録する必要はありません。過去問では「小問ごとの配点が分からない」「記述の採点基準が分からない」ということが普通なので、ザックリ正答率を記録しておけばOKです。
得点を記録しておくと、「他の年度と比べてどれだけ成長できたか」「今の自分は平均してどれくらい解けるか」を把握できます。最終的に志望校に受かるかを判断する基準となるため、自分の得点は把握しておきましょう。
ステップ5.間違えた問題を解説を閉じて解きなおす
得点の記録まで終わったら、解説を閉じて間違えた問題をもう一度解き直しましょう。
スラスラと解答できれば、間違えた部分もしっかり身についている証拠です。もし、解説を閉じて解けなければ、解説の読み込みが足りず理解できていないことになります。
仮に理解できていなかったとしても、落ち込みすぎないようにしましょう。何度も解説を読んで、解き直して、最終的にしっかり理解できればOKです!
ステップ6.苦手分野が見つかったら問題集で苦手を克服する
過去問演習を続けていくと、

という単元・分野が出てくるでしょう。
何度も間違えてしまう部分は、あなたの苦手な分野です。苦手分野を把握したら、もう一度問題集に戻って、苦手な部分を集中的に勉強しましょう。
数学の過去問演習に関するよくある質問
最後に、数学の過去問演習についてよくある質問についてまとめました!自分の疑問点がないかをチェックしておきましょう。
Q1.過去問演習って何年分くらい取り組めば良いの?
正直なところ、過去問演習に取り組む回数は「多ければ多いほうが良い」のが事実です。とはいえ実際は、学校に通いながら受験勉強を進めるわけなので現実的なラインを見極めまる必要があります。
参考までに、志望校の種類別で過去問に取り組む回数をまとめました。
国公立志望の場合
まず共通テスト対策は「10年分」が1つの目安です。まだ共通テストの実施回数は少ないので、模擬形式の問題集や直前パックなどを使って勉強します。
1〜2回目くらいで目標点数が取れたとしても、最低でも5年分は取り組みましょう。逆に目標点数に全然届かない場合は、10年分を最低ラインとして「2〜3周目に取り組む」「もっと回数を増やす」というのもありです。
次に、個別試験は「第1志望の過去問は10年分」くらいは取り組みたいところ。赤本に3年分くらいしか過去問が載ってなくても、中古でいいので入手しておきます。学校の進路指導で借りるのも良いですね。
ただし、滑り止めも考えると、現実的には「5年分くらい」しかできない人も多いはず。その場合も、5年分は本当に「合格に必要な最低限のライン」なので、多少無理してでも5年分は下回らないようにしてください。
これに加えて、滑り止め校も「各大学5年分ずつ」は取り組んでおくと良いですね。
私立志望の場合
私立専願の場合は、併願大学数が国公立志望よりも多くなるため、科目数が少なかったり共通テストが必要なかったりしても、そこまで楽にはなりません。
基本的には国公立大を目指す人と同じで、「第1志望は10年分を目標」「併願大学は5年分を目標」として過去問演習を進めましょう。
浪人できない現役生の場合、偏差値の低い大学から順に過去問をこなしていき、「この大学は合格最低点を安定して超えられる!」という状態を作りながら進めることがオススメです。
もしも5年分演習しても合格最低点を超えられない場合、その大学を滑り止めとするには不安が残ります。その場合は、どこの大学を受験するか改めて考えましょう。
Q2.過去問演習っていつからはじめれば良いの?
遅くとも「高3の11月中旬から」は過去問演習をメインに勉強することが理想です。すでに出遅れている人は、今日からガンガン進めていきましょう。
11月中旬以降は、中途半端な所までしか進んでいない参考書を切り上げてでも、過去問演習メインの学習に入ってください!
仮に12月スタートになってしまった場合は、できる限り休むことなく淡々と演習を続けてほしいところです。
Q3.過去問の復習にはどれくらい時間をかけるべき?
過去問演習の復習には、「過去問を解いた時間の倍の時間」まで使いましょう。過去問演習は入試を想定した練習であるため、ここで明確になった苦手分野は、徹底的に復習して克服する必要があります。
細かいところまでチェックし、参考書や問題集で公式などの確認まで行うと、試験時間の2倍でも足りないかもしれません。とはいえ、復習に時間をかけすぎると過去問演習のペースが落ちるため、「試験時間の2倍」を上限としましょう。

まとめ
受験数学の勉強は、過去問演習まで取り組むことで完成します!入試本番と同じように制限時間を意識しつつ、確実に取れる問題を落とさないことが重要です。
問題演習で積み重ねた知識を本番でしっかり活用できるよう、過去問を最低でも10年分(どんなに少なくても5年分)は繰り返し解いて本番までに出題傾向を把握し、緊張せずに挑める準備をしておきましょう!
もっと具体的に「このとおりに勉強すれば数学の勉強は完璧、という参考書の流れが知りたい!」という方は、ぜひSTRUXの参考書マップを活用してください!

■ 参考書マップとは? ■
STRUXの「参考書マップ」は、受験までにやるべき勉強を「順番通りに」すべて洗い出したもの。「いつまでに」「どの順番で」勉強をすればいいかがひと目で分かるので、あとはこの通りに勉強するだけ!という状態になります。
- 「どの順番で」参考書に取り組めばいいかひと目でわかる!
- 「なぜこの参考書がおすすめなのか?」「かわりに使える参考書」もすべて紹介
STRUX参考書マップ公式LINEに登録することで、いつでも無料で見ることができます!
LINEに登録して参考書マップを見る













