三角関数ってなかなか難しいし理解もしにくいですよね。この記事では、「公式がいっぱいで大変……。」とか「結局何が重要なの？」といった皆さんが持っている三角関数への悩みを解決していきます！
公式の覚え方に関しては以下の動画でも詳しく解説しています！
戦略1 三角関数は三角比の復習から始めよう！
- 直角三角形があったとき、$\sin \theta , \cos \theta , \tan \theta $がそれぞれどこを指すかわかる
- $ \sin^2 \theta + \cos^2 \theta = 1 $、$ 1 + tan^2 \theta = \frac { 1 }{ \cos^2 \theta } $という公式を覚えている
- 正弦定理と余弦定理がどんな公式だったか覚えている
- 三角比を用いて三角形の面積が出せる
戦略2 2つのポイントを押さえれば三角関数の基本がわかる！
いろいろな公式があって、何がしたいのかわからない問題って多いですよね。でも、三角関数の問題って突き詰めていくと意外にシンプルで、重要なテーマが2つに絞れるんです。三角関数でよく狙われるテーマは、「三角関数を用いた方程式・不等式」と「三角関数の最大・最小」です。もちろん、これよりむずかしい問題もありますが、今回はよく出題される＆三角関数を勉強する上で基礎になるこの2テーマをおさえましょう！
①三角関数を用いた方程式・不等式
例としてはこんな問題があります。
$ 0 \leqq \theta \leqq 2 \pi $のとき、
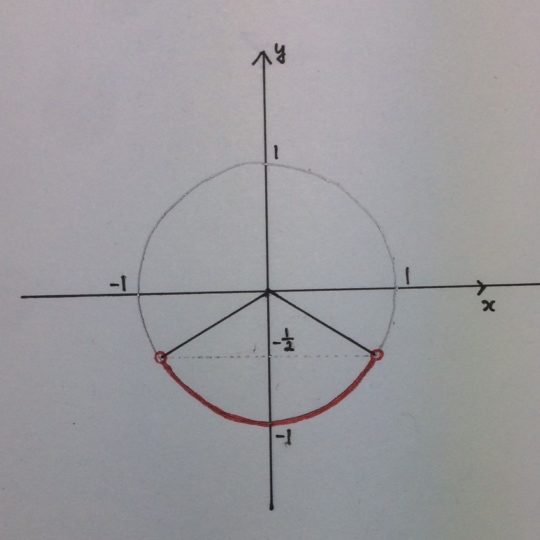
(1) $ \sin \theta \lt – \frac { 1 }{ 2 } $を解け
(2) $2 \sin^2 \theta + \sin \theta -1 = 0 $を解け
このような問題を解くときに重要なのは、座標を見たときに $\sin$ は$y$軸上、$\cos$は$x$軸上にあらわれると言うことです。このことさえわかっていれば問題は解けます。
メモとして単位円を書き考えることでイメージがつかみやすくなります！たとえば、(1)ならこんな感じです。
②三角関数の最大・最小
もうひとつのテーマは最大・最小。こんな問題を見たことはないでしょうか？
$ 0 \leqq \theta \leqq 2 \pi $ のとき、
$ y = \sin ^ 2 \theta + 2 \sin \theta + 1 $ の最大値・最小値を求めよ。
こんな問題を解くときには「置き換え」が使えます。
例えば、この問題では、よく解いていた2次関数と同じようにするため、$\sin \theta = x$ としましょう。$ x $の2次式なら解けますよね。
いいんです。ただ、置き換えるときは、変数を変数に置き換えることに注意しましょう。例えば今回は、$\sin \theta$という変数を$x$という変数に置き換えましたね。問題によっては$ \cos \theta $や $ \sin \theta \cos \theta $、$ \sin \theta + \cos \theta $や$ \sin \theta – \cos \theta$を$x$に置き換えるなどいくつかのパターンがあります。
ただ、後の3つは難しいので、センター試験であれば問題文に置き換えの方法が書いてあることがほとんどです。
また、どう置き換えればいいのかわからない場合は、いくつか試してみることが大事です。最初から上手く置き換えができる人はいません。2次試験の勉強をする際でも、最悪全部試してしまえば解けるというわけです。
そして、置き換えをしたときには1つ、注意しなければいけないことがあります。それは置き換えた後の$x$がどの範囲を動くか、ということです。
今回で言えば$ 0 \leqq \theta \leqq 2 \pi $のなかでの$ \sin \theta $が$x$に等しいんですよね。$ 0 \leqq \theta \leqq 2 \pi $の範囲で、$ -1 \leqq \sin \theta \leqq 1 $ですから、$x$が2とか100とかの値だったらおかしいですよね。
つまり、$x$にも範囲の限定があるわけで、今回で言えば$ -1 \leqq x \leqq 1$なんです。このことにさえ注意すればあとは2次関数と同じように解くだけです。
$\begin{eqnarray} y = x^2 + 2x + 1 \\ y = ( x + 1 )^2 \\ -1 \leqq x \leqq 1より\end{eqnarray}$
最大値は$ x ＝ 1 $のとき、4
最小値は$ x = -1 $のとき、0
こんな風に解けてしまいます。
『勉強法は分かったけど、志望校に合格するためにやるべき参考書は？』
『勉強法はわかった！じゃあ、志望校に向けてどう勉強していけばいいの？』
そう思った人は、こちらの志望校別対策をチェック！
戦略3 三角関数で得点を取るために
①公式を覚えよう！
教科書にのっている公式は基本的にすべて覚えましょう。和積公式、積和公式は加法定理から導けるので後回しにしても構いませんが、それ以外の公式はかならずすべて覚えて下さい。
三角関数は他の分野と比べても特に、公式を覚えていないと手も足も出ない分野です。教科書にはさまざまな公式がのっていますが、それらをすべて覚え、使えるようになっていることがこの分野の前提です。
これは平成29年度センター試験数学ⅡBです。
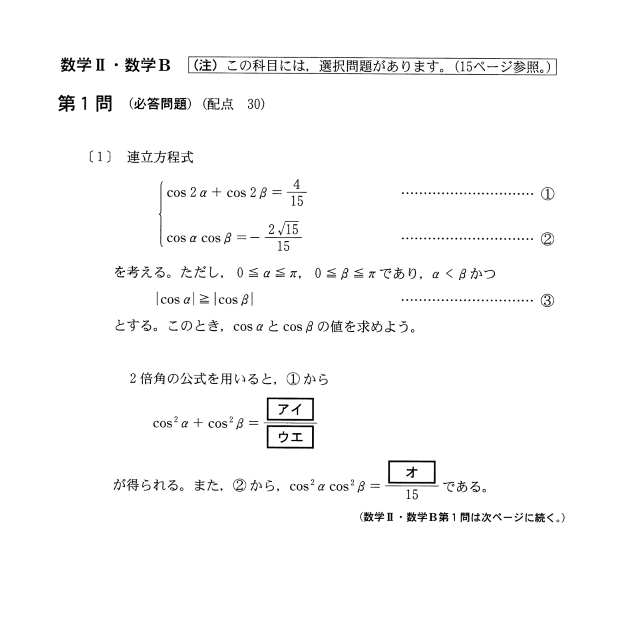
例えばこれがいい例ですよね。センター試験で大問Ⅰのアから公式そのまんまです。
一番いいのは教科書を読んで内容を理解し、参考書などの例題で実際に使ってみることです。理解しないまま覚えてもすぐに忘れてしまいますし、実際に使ってみないと本当に身についているのかどうか判断ができません。三角関数のなかでひとつでも不安な公式がある人は、まず教科書を読み、例題などを解いていきましょう。
②公式を身につけよう！
教科書で公式を覚えたら、チャートやフォーカスゴールドの基本問題を演習していきます。この勉強はできるだけ早い時期から行いましょう。一番いいのは三角関数を習ったとき、教科書の理解と同時に演習します。それができなければ定期テストの前や長期の休みなどにまとめて勉強しましょう。
③センター試験対策！
センター試験の問題は教科書の問題よりも様々な要素が入っており、間違えてしまうことも多いです。そんなときには、間違えた理由を分析しましょう！
センター試験で出題される三角関数の問題は、
(1)まず公式を使って式を簡単な形に変形させ、
(2)戦略2で紹介したような基本の2パターンの形にして解く
という2段階構成のものがほとんどです。
ですから、自分ができなかったのは、(1)なのか(2)なのかを判断しましょう。
(1)ができていなければ教科書で公式を覚えた後にチャートなどで勉強します。
(2)ができていなければ置き換えができなかったのか、式が解けなかったのかなどの分析をし、解けるようになるまで復習しましょう。
青チャートカリキュラム(執筆中)
センター試験は似たような設定の問題や、考え方が同じ問題が何度も出題されます。ですから、センター試験で高得点をとるためには、一度解いたことのある問題を2回目以降で間違えないことが重要です。間違えた問題はしっかりと復習して、解けるようにしておきましょう！
④2次試験対策！
青チャートやフォーカスゴールドを一通り解いたけれど、2次試験レベルになるとうまくいかないという人は問題演習の量を増やしてみましょう。これは三角関数に限らず数学のあらゆる分野でいえることですが、問題演習しなければ学んだことを生かせるようにはなりません。いまから紹介する参考書で練習していきましょう！
(1)青チャート 数学Ⅱ
★2~3だとセンター試験レベルの典型問題ですが、★4~5になると応用問題や入試レベルの問題がそろっています。典型問題を練習したら、そのまま難しい問題にも挑戦しましょう！
(2)文系数学の良問プラチカ 数学1A2B
解説の丁寧さで長く支持されている参考書です。わからなかった問題でも解説をしっかり読めば自分一人で演習が積めます！使う時期としてはチャートが終わってからで大丈夫。定石が身についてから入試問題の演習に入るまでに勉強しましょう！
応用演習リンク(執筆中)
それでも勉強法がわからない！という人は
三角関数のもっと細かい覚え方のコツとか知りたい！数学のもっと具体的な勉強法を教えて！そんなときはLINEで質問！このほかにも限定コンテンツを配信中！まずは友だち追加↓
まとめ
- まずは三角比の復習から！
- 公式は教科書で理解し、問題集で使って覚えよう！
- 「三角関数を用いた方程式・不等式」と「三角関数の最大・最小」の2パターンをマスターしよう！
もっと具体的に「このとおりに勉強すれば数学の勉強は完璧、という参考書の流れが知りたい！」という方は、ぜひSTRUXの参考書マップを活用してください！
■ 参考書マップとは？ ■
STRUXの「参考書マップ」は、受験までにやるべき勉強を「順番通りに」すべて洗い出したもの。「いつまでに」「どの順番で」勉強をすればいいかがひと目で分かるので、あとはこの通りに勉強するだけ！という状態になります。
- 「どの順番で」参考書に取り組めばいいかひと目でわかる！
- 「なぜこの参考書がおすすめなのか？」「かわりに使える参考書」もすべて紹介
STRUX参考書マップ公式LINEに登録することで、いつでも無料で見ることができます！
LINEに登録して参考書マップを見る
