【数学1】集合と命題｜ 高校数学最初の関門？集合と命題を突破する勉強法

「記号が多くてわけわからない……」、「ドモルガンの法則って結局どういうこと！」など悩んでいませんか？高校数学で最初の関門となることが多い集合と命題の勉強法のコツをお教えします！

• 
• 案件
  集合と命題の問題が解けません。

赤神さん～もう数学嫌だぁぁ～

どうした？まだ高校数学始まったばかりじゃないのか？

そうなんだけど集合と命題ってわけわからなすぎてもう嫌！

まぁ確かに集合と命題は確率と並んで高校数学最初の関門となることが多い分野だ、無理はないな。さきさきはどこでつまずいているんだ？

記号が多いし見た目じゃ全然わかんないし覚えられないの～

なるほど、確かに記号が多く出てくるしわかりにくいな。だが逆に記号さえ覚えてしまえば集合と命題はほとんど押さえたも同然だぞ！わかりやすく伝えるからついてこい！

おけまる～うち頑張っちゃうんだから！

戦略1. 集合の記号と言葉の定義を確認しよう

1-1集合ってそもそも何？

集合について勉強していく前に、まず集合という言葉の定義を確認してみましょう。

ちょっこれなに言ってるの～赤神さん日本語訳して～

いやこれ日本語だからな。まぁそんなことはどうでもいい。
次の2つが集合と呼べるかわかるか？

「1~10の整数」
「大きい数」

うーん最初のは集合で2つめのは違うかな？

そうだ。1つ目は1~10の整数という具体的な定義があるが、2つ目の大きな数という定義は具体的ではないから集合とは言えない。「大きな数」といっても100以上は大きい数だと思う人もいるし1000でも大きい数とは言えないと思う人もいるから、大きな数というだけではそれがなにを指しているのか決まらないのだ。

えーっとつまり、はっきりとした定義があるものの集まりを集合っていうってこと～？

そういうことだ。そして集合を構成しているもの1つ1つのことを要素(または元)ということも押さえておこう。

要素が集まって集合になってるってことね。おっけ～

ここまでをまとめると次のようになるな

集合：定義が具体的に示されているものの集まり
要素：集合をつくる1つ1つのもの

1-2集合の表し方

集合という言葉の定義を確認したところで集合を表す時の書き方について説明しよう。 集合の書き方には次の2つの書き方があるぞ

例.)1~10の整数という集合A
①A＝{1,2,3,4,5,6,7,8,9,10}
②A＝{x|1≦x≦10,xは整数}

え？なにこれ意味わかんないんだけど。

1つずつ解説していくからそう焦るな。まず①は集合の要素を1つずつ並べるという書き方だ。要素が多い時とかは「……」を使って省略することもできる。今回の例だとA={1,2,……9,10}の様に表せる。

1つずつ書いていけばいいだけなら単純ね！

②は要素がどういう条件を満たしているかを示す書き方だ。”|”という縦線の左側でxが要素の代表ですよーと書いて、右側でそのxはこういう条件を満たしています、と書くのがこの書き方だな。xは条件を示す時に使いたいから要素の代表として置いているだけなのであまり深く気にしなくていいぞ。

今回だと「1≦x≦10」と「xは整数」の部分が条件ってことね！

そういうことだ。しっかり理解できているな！

1-3記号の定義を確認しよう

いよいよ集合のカギとなる記号を紹介します。ここを押さえれば集合はマスターしたといっても過言ではないのでしっかり勉強していきましょう！

いよいよ集合の肝となる記号の定義を見ていくぞ。ここで紹介するのは次の6つの記号だ。「∈」「⊂」「∩」「∪」「∅」「$ \overline{A} $」

だーかーらーいきなり難しい話しないでって！

まぁ落ち着け。一気に6つ学ぶのは大変だから以下の2つずつ3つのグループに分けて学ぶぞ。

ⅰ) 「∈」「⊂」

これらは集合の要素や集合同士の包含関係(含む含まれるの関係)を表すのに使われる記号だ。
1つ目の記号∉は「a∈A」のように使って、「aは集合Aに属する」という風に読むんだ。
意味としては「aは集合Aの要素である」ということを表す。

1-2の例(Aは1~10の整数の集合)でいうと「1∈A」っていえるってこと？

そういうことだ。ちなみに∈はelement(要素)の頭文字からきているぞ。

ん、英語苦手だからパス。

……まぁいいか。2つ目の記号⊂は「A⊂B」のように使って、「AはBに含まれる(BはAを含む)」という風に読む。意味は「AはBの部分集合である」ということになる。

部分集合ってなにー教わってないよー

部分集合というのは2つの集合の関係を表す言葉で、AがBの一部（あるいは全部）の要素だけできていることを意味していて、AがBの一部分であるという意味で部分集合という風に言うんだ。

うーんまだいまいちわからない～

例を挙げよう。「Aは1~10の偶数の集合」「Bは1~10の整数の集合」という集合A,Bを考えると、Aの要素は2,4,6,8,10、Bの要素は1,2,3,4,5,6,7,8,9,10でAの要素はすべてBに含まれているな？こういうときA⊂Bと表せるんだ。

Aの全部の要素がBの要素に含まれていればいいのね！

ⅱ) 「∩」「∪」

次はこの2つの記号だ。これらの記号は2つ以上の集合の和や共通部分を表す記号だ。具体的に見ていくと1つ目の記号∩は「A∩B」という様に使い、「AかつB」と読む。意味はAに属しかつBにも属する集合ということだ。

んんん？ちょっと待って1回整理させて～
Aが1~5の整数の集合でBが奇数全体の集合だとしたら、A∩Bは1~5の整数かつ奇数ってことはその共通部分は……1,3,5を要素にもつ集合ってことであってる？

正解だ。AとB両方の要素であるというのが∩の意味だと覚えてもらえれば大丈夫だ。
2つ目に移ろう。2つ目は∪という記号だがこれは「A∪B」で「AまたはB」と読んで、「AかBかどちらかには属している要素の集合」という意味になる。

AまたはBってことはAとB両方に属している要素は除外されるの？

いや除外されないんだ。ここが落とし穴となりやすいんだが、日本語でAまたはBという時、多くの場合は「AかBかのどちらかだけを満たす」ことを表すが、A∪Bでは「AかBかのどちらかだけ＋AかつBである」ことを表すんだ。分かりにくいだろうから∩と合わせてベン図にまとめておいたぞ。

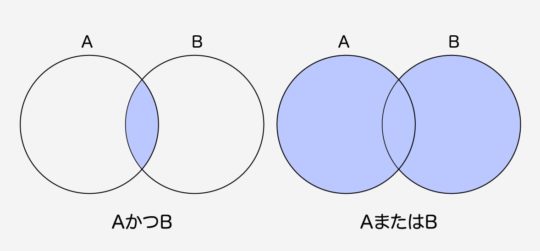
わかんなくなったらお絵描きすればいいのね！おっけ～

ⅲ) 「∅」「$ \overline{A} $」

最後はこの2つの記号だ。これらは集合の少し応用的な部分だが、しっかり定義を確認すればそんなに難しくないからゆっくり確認していこう。
まず1つ目の∅だが、これは空集合といい、属する要素が1つもない集合を表す。

属する要素が1つもない集合ってどういうこと～？

少し理解しにくいかもしれないから例を挙げよう。さきさき、「3以上で2以下の整数の集合」を求めろと言われたらどうする？

3以上で2以下なんてそんなのあるわけないじゃん！

そうつまり空集合「∅」は要素が存在しない集合を表すのだ。

うーんなんとなくわかったかも？

まぁ後でもう1回まとめておくからしっかり確認しておくんだぞ。つぎは2つ目の$ \overline{A} $についてだが、Aの補集合といって、「Aでないものの集合」を表す。

うーん……？AじゃないってことはAが偶数の時だったら奇数の集合を表すってこと？

そういうことだな。さらに厳密にいえばAの補集合は「全体集合の中でAでないものの集合」というふうにいえる。

全体集合ってなに！普通の集合となにがちがうの～

うむ、説明しよう。全体集合は記号Uで表す。ここでU={x|xは整数}という全体集合Uを考えよう。このとき「この問題では、全体集合U={x|xは整数}が、ここで存在する数字のすべてだと考えてね」という意味がある。つまり整数以外は存在しないと考えていいということだ。

小数とかはその問題では存在を無視しちゃうってこと～？

そういうことだ。さっきAが偶数の集合ときAの補集合は奇数の集合だとさきさきは言っていたが正確に言うとあれは全体集合Uが整数の集合のときに限られるな。
1-3で出てきた記号をまとめておいたからしっかり復習しておくんだぞ！

はーい

a∈A

aは集合Aに属する要素の1つである

A⊂B

集合Aは集合Bの部分集合である(Aの要素はすべて集合Bに含まれる)

A∩B

集合Aにも集合Bにも属する要素の集合

A∪B

集合Aか集合B少なくともどちらかには属する要素の集合

∅

要素を1つももたない集合

$ \overline{A} $

全体集合Uの要素の中で集合Aの要素ではないものの集合

戦略2. 命題は、逆,裏,対偶を押さえよう

逆,裏,対偶と聞いて頭を抱える人も多いのではないでしょうか！？逆,裏,対偶がそれぞれ何を指しているかよくわからなくなってしまっている人も多いはず！ 命題の分野では多くの人が逆,裏,対偶でつまずいています。逆に逆,裏,対偶を押さえてしまえば命題は怖くありません！ゆっくり丁寧に確認していきましょう！

2-1命題とは？

逆,裏,対偶の説明の前にまずは命題の基本事項の確認から行っていきましょう。
まずは命題という言葉の定義から確認しましょう

赤神さん～わかりやすく！

そう言われると思って例を用意しておいたから安心しろ。
例えば「4は偶数である」というのは正しいということが明確にわかるから命題といえるが、「100は大きい数である」というのは命題とは言えないのがわかるか？

うーんなんとなく……？人によって大きいか小さいか判断が分かれるからってこと？

そういうことだ。大きい数の基準は人によって違うから100が大きい数かどうかを明確に判断することはできない、つまり命題ということはできないんだ。

なるほど～おっけー！

命題がわかったところで次に進もう。命題が正しいと判断されたとき、その命題は真であるといい、逆に誤っていると判断されたとき、その命題は偽であるという。

えーっとさっきの「4は偶数である」って命題は正しいから真ってことね

そうだ。「4は奇数である」という命題があったらそれは偽だな。
ここまでをまとめておこう

命題

正しいかどうかを明確に判断できる主張のこと

真

命題が正しいこと

偽

命題が正しくないということ

次は命題の表し方だな。命題はさっきの「4は偶数である」みたいに文章で表すときと、「A⇒B」という風に記号で表すときがある。「A⇒B」は「AならばB」と読む。

いきなり出てきたけどAとかBとかってなに～

AやBは条件と呼ばれる部分だな。例えば「x=1⇒x>0」という命題があったらAやBにあたるのはどの部分だと思う？

A⇒Bってことは、Aがx=1でBがx>0？

そうだ。Aはx=1という条件を表していて、Bはx>0という条件を表している。
またAは仮定、Bは結論とも言われる。Aは「とりあえずx=1のときの話ね」という仮定で、Bは「x>0っていうのがこの話の結論ね」という結論を表しているからそう言われる。

仮定⇒結論、矢印の元が仮定で先が結論ってことね！

ちなみにA⇒Bという命題が真のときA(仮定)を十分条件、B(結論)を必要条件ということも覚えておこう。わかりにくいと思うからさっきの例で考えてみよう。
「x=1⇒x>0」において十分条件と必要条件はそれぞれなにになる？

えーっと命題が真だったら⇒の左側が仮定でーそれが十分条件だからー「x=1」が十分条件で、⇒の右側が結論で必要条件ってことは「x>0」が必要条件ね！

正解だ。⇒の右か左かで覚えておくとわかりやすいな！

十分条件

命題が真のときの仮定(⇒の左側)

必要条件

命題が真のときの結論(⇒の右側)

2-2真偽判定とその証明

命題とはなにかについて学んだあとは、命題の分野で問われることが多い命題の真偽判断とその証明問題について学んでいきましょう！

赤神さん～命題の真偽判定ってなに～？

おっけー、そこから解説していこう。さきさきはこんな問題を見たことないか？

「次の命題の真偽を答えよ、ただしxは整数とする。命題：$x^2=4$ のとき $x=2$である」

あーそれなら見たことある！いつも答え方がよくわかんないの～

そういう悩みは結構多いな。例えばさっきの問題はどうだ？

うーんx=-2のとき成立しないから偽？

正解だ。反例をあげることができるものは答えが偽となるな。問題は答えが真になるときの答え方だ。ただ単に「答え：真」と答えるだけじゃなくて証明もしなければいけない。

えー証明とか大っ嫌いなんだけど～

まぁそう言うな。これからちょっとしたコツを教えるからしっかり聞いてくれよ。

はーい

コツとは証明しにくいと思ったら集合で考えてみるということだ。

集合ってこの記事の戦略1でやったやつね！

そうだ。例えば次の問題を考えてみよう。

「命題：0≦x≦1⇒|x|≦1　の真偽を答えよ。(ただし真の場合は証明を、偽の場合は反例を挙げよ)」

うーんパッと反例が浮かばないからたぶん真だと思うけどぉ証明できない～

そこでさっき言った集合の考え方を使うぞ。まず仮定の部分の0

あっ0≦x≦1は-1≦x≦1に含まれているから真で大丈夫なのね！

そう、集合で考えたときに仮定にあたる集合が結論にあたる集合に含まれていれば真といえるんだ。そして証明も楽になるぞ。今回でいったら次のように答えればいい

解答
集合A,Bを以下のようにおく。
A={x|0≦x≦1},B={x|-1≦x≦1}
ここで題意の命題の仮定0≦x≦1は集合Aと同義であり、結論|x|≦1は集合Bと同義である。また、A⊂Bであることから0≦x≦1⇒|x|≦1は真である。

証明しにくい命題の真偽判定の問題は集合を使って考えれば楽なのね！

2-3逆,裏,対偶

さて、いよいよ本題だ。これから逆,裏,対偶について説明するが、この章では全部「$x=1⇒x^2=1$」という命題を例に説明するぞ。とりあえずそれぞれの言葉の定義を以下に説明する。

A⇒Bに対して

逆

B⇒A($x^2=1⇒x=1$)

裏

$ \overline{A} \Rightarrow \overline{B} (x\neq1 \Rightarrow x^2\neq1)$

対偶

$ \overline{B} \Rightarrow \overline{A} (x^2\neq1 \Rightarrow x\neq1)$

裏と対偶のところにある$\overline{A}$とか$\overline{B}$ってなに？

集合のところでも出てきた記号だが、$\overline{A}$や$\overline{B}$は否定を表している。つまり$\overline{A}$だったら「Aじゃない」という意味になる。今回Aはx=1だから$\overline{A}$は$x\neq1$になるな。

ねーこれ逆って成立してなくない？「$x^2 = 1 \Rightarrow x = 1$」ってダメじゃん。

そう、命題が真だからといって逆や裏も真であるとは限らないんだ。
だが、命題が真のとき対偶は必ず真になる。命題の真偽と対偶の真偽は必ず一致するんだ。
下にベン図を示したからそこで確認しよう。

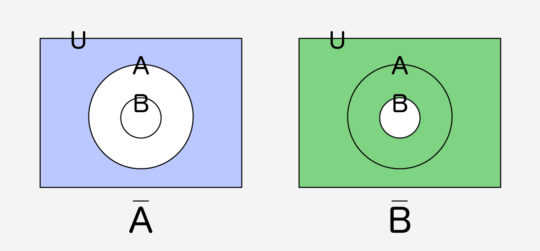
また逆,裏,対偶は次のような関係になっている。これらの関係もしっかり確認しておこう。

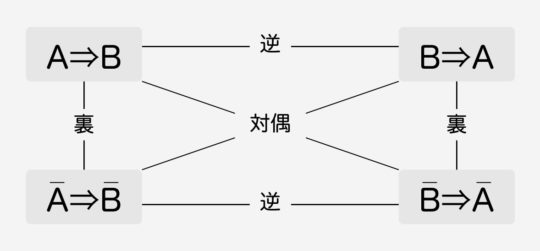
逆と裏のどっちがどっちかわかんなくなったら「逆はもとの矢印を逆にする」と覚えておこう！

『勉強法は分かったけど、志望校に合格するためにやるべき参考書は？』
『勉強法はわかった！じゃあ、志望校に向けてどう勉強していけばいいの？』
そう思った人は、こちらの志望校別対策をチェック！

志望校別対策はこちら

まとめ

最後にポイントを振り返りましょう。

①集合は「∈」「⊂」「∩」「∪」「∅」「$\overline {A}$」の6つの記号の意味を押さえる

②命題は逆,裏,対偶の意味と関係性を押さえる

教科書と問題集の勉強法は以下のリンクを参照してください！

教科書を理解するのが絶対必要！数学の教科書レベルの勉強法

集合と命題を得意にして高校数学のスタートダッシュを成功させましょう！

もっと具体的に「このとおりに勉強すれば数学の勉強は完璧、という参考書の流れが知りたい！」という方は、ぜひSTRUXの参考書マップを活用してください！

■ 参考書マップとは？ ■

STRUXの「参考書マップ」は、受験までにやるべき勉強を「順番通りに」すべて洗い出したもの。「いつまでに」「どの順番で」勉強をすればいいかがひと目で分かるので、あとはこの通りに勉強するだけ！という状態になります。

• 「どの順番で」参考書に取り組めばいいかひと目でわかる！
• 「なぜこの参考書がおすすめなのか？」「かわりに使える参考書」もすべて紹介

STRUX参考書マップ公式LINEに登録することで、いつでも無料で見ることができます！

LINEに登録して参考書マップを見る

数学全体の勉強法はこちらから