高校数学最初の難関である2次関数。苦手な人も多いのではないでしょうか。2次関数は、今後の高校数学のいろんな分野で当たり前にその考え方や計算を使います。それに、センター試験にも頻出です。この記事では、「2次関数とは何か」から具体的なパターンや勉強法にいたるまで、詳しく解説。2次関数をどうにかしたい、という人は必見です!










戦略01 そもそも2次関数って何??
さて、2次関数の勉強法の説明に入る前に、そもそも、

という人も多いでしょう。そんな人のために、2次関数を解く上で必要な用語や基本事項を軽く説明しましょう。そんなのはさすがに余裕、という人は、とばして戦略02にいっても構いません。
2次関数とは
まず、関数には、「変数」と呼ばれるものが含まれます。
変数は、その名の通り、「変わりうる数」のこと。1なのか2なのか10000なのか、どんな数字が入るかわからないので、xやyといった文字を用いて表します。(ちなみに変数の対義語は「定数」と呼ばれ、これもその名の通り「定まった数」なので、値が1つにあらかじめ決まっています。)
そして、そのxの値が1つに決まったとき、同時にyの値も1つに決まるとき、yはxの関数である、という言い方をするのです。これを数式で書くと、 $y=f(x)$ と表します。
xの値が定まれば、yの値が決まる、ということは、yはxを用いて表せる、ということですね。たとえば、y=2x+1と表せるなら、xが1であればyは3に決まります。つまり、関数とは、簡単に言ってしまえば、
関数=“xとyの関係を表す式”
なのです。数学的に厳密な定義ではありませんが、苦手な人はまずこれで構いません。
ではなぜ、「2次」関数と言うのでしょう?さきほどy=2x+1という式が出てきましたが、これはどういう関数でしょう??

そうです。中学でやりましたね。y=2x+1ではyはxの1次式で表されています(1次式というのは変数に2乗とか3乗とか√とかがついていない式のこと)。ということは……。
2次関数=“yがxの2次式で表された関係式”
というわけです。たとえば、$y=x^2-3x+1$はまさに2次関数です。
定義域と値域

サキサキのように、変数ってどんな値でもいいのか?と気になる人もいるでしょう。
まず、問題で特に指定がなければ、変数の取りうる値は、実数の範囲では自由です。
ですが、たとえば問題の中で$0\leqq x \leqq2$のように指定があるときがあります。このように、変数のうち$x$のとりうる値の範囲のことを,定義域、逆にyのとりうる値の範囲のことを値域といいます。
平方完成
2次関数でよく使う重要な式変形に「平方完成」というものがあります。

カンタンに言えば、2次関数はさきほどの問題にもあった通り、$y=x^2-6x+5$のように、$y=ax^2+bx+c$という形で提示されることがほとんどです。
しかし、2次関数のグラフをかくときなど、このままでは困ることがあります。そこで、この式を$y=a(x-p)^2+q$という形にするのです。これを平方完成と言います。

この式の形にすることで、2次関数のグラフ、すなわち放物線の軸と、頂点の座標がわかるわけです。さきほどの式で実際にやってみると、
$y=(x-3)^2-4$
のような形になるんですね。この場合、軸はx=3、頂点の座標は(3,-4)になるわけです。これで、2次関数のグラフをかくことができます。



戦略02 2次関数のお決まり問題3パターン+コツ



- 2次関数の最大値と最小値を求める問題
- 2次関数と直線、あるいはx軸との位置関係に関する問題
- 2次関数を平行移動する問題


2次関数の最大値と最小値を求める問題
もっとも頻出なのがこれ。最初にサキサキが悩んでいたのもこのタイプの問題でした。
このタイプの問題でのポイントは、たった2つのキーワードに集約されます。
それは、「定義域と軸の位置関係」と「グラフを描く」です。
定義域と軸の位置関係
まずは、「定義域と軸の位置関係」について。以下の2つの放物線は、同じものですが、定義域が違います。さて、最小値は同じでしょうか?
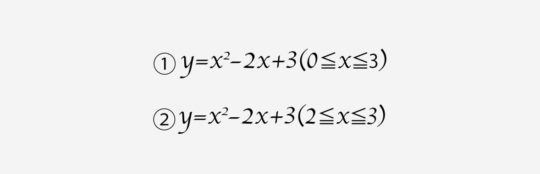
答えは、左の方の最小値は2で、右の方では3ですので、最小値は異なります。ではなぜ違うのでしょう?
これは、頂点、すなわち軸の値が、定義域に含まれているか含まれていないか、による違いです。
下に凸の放物線をパッと見たら、頂点の部分、すなわち軸で最小値をとりそうなことはすぐわかるでしょう。しかし、その頂点のx座標が定義域に入っていなければ、その部分は存在しないも同然なので、違うところに最小値がくるわけです。
では、上の図の左の放物線の最大値はいくつでしょう?最小値は頂点ですから簡単でしたが……。
ポイントは、放物線が左右対称である、という点にあります。左右対称ということは、軸から離れるほど、どんどん値が大きくなっていく、ということですね。
つまり、候補は定義域の両端の2つの点でしょう。このうち、より軸から離れている方を選べばいいのです。


グラフを描く
次に、「グラフを描く」について。2次関数を図形的に表すと放物線になる、というのはさきほど戦略01でやりましたが、最大値と最小値を考える上で、グラフを描くことは超重要です。
せっかくなのでサキサキが悩んでいた問題を例にとってみましょう。

これを瞬時に解ける人は、そうそういません。けれど、次のようになっていたらどうでしょう。
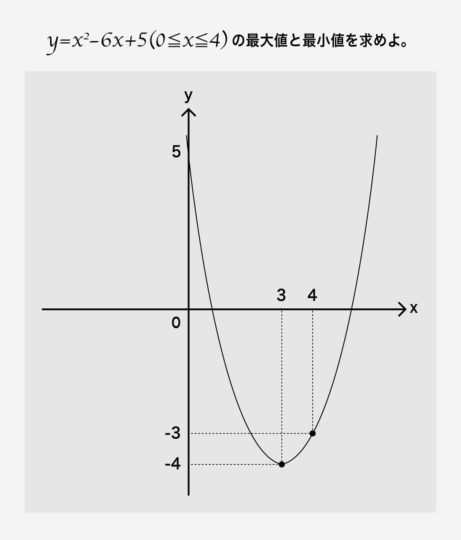
答えとなる最大値と最小値はともかくとして、$x$がどんな値のときに最大or最小になるかは、一目瞭然ですね。このように、グラフは、視覚的に最大値と最小値をとる場所を把握する上で、とても役立つのです。
そして、実はグラフは、自分にとってわかりやすいだけでなく、答案を記述式で書くときに、採点者にとってわかりやすい答案を書くのに必須のものでもあります。なぜなら、視覚的に一発で、この答案は何をしているのかがわかるからです。そのため、グラフを描くだけで部分点がもらえたり、逆に描かないと逆に減点されたりすることもあります。

サキサキのように思う人もいるでしょう。確かに、x軸とy軸を描いて、x切片やy切片に注意しながら放物線を描いて……、というのは手間がかかります。それに、参考書に載っている図と違って答案は基本黒一色しか使えないので、定義域や最大値をとる点を赤で塗って……といったこともできません。

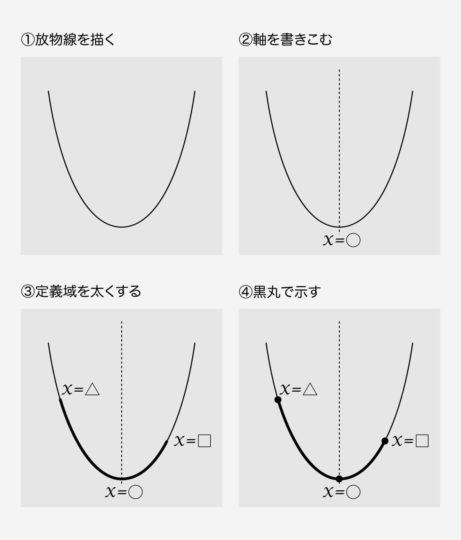



2次関数と直線、あるいはx軸との位置関係に関する問題
まず、2次関数と直線の位置関係に関する問題として、

……という問題があります。



このときにポイントとなるのは、
放物線と直線の共有点と、2つの式のyを消去して得られる2次方程式の実数解には対応関係がある、ということです。
つまり、

と言えるわけです。2次方程式の実数解の個数を求めるときに使うのは……、そう、判別式ですね。





このタイプの問題では、たった3つのことに気をつければ良いです。それは、
- 判別式
- 軸
- 端点の値
です。

端点の値とは、言葉を付け足すと、「注目している範囲の端の点の値」です。
上の問題では正の部分、というのが注目している範囲ですから、端点は$ x = 0 $の点、となります。

問題によっては、3つのうちどれかだけを調べれば答えにたどりつく問題もあります。それは演習をするうちに見抜く力をつけていきましょう。


2次関数を平行移動する問題
たとえば……こんな問題



サキサキのようにグラフを実際に書いてみるのもありですが、それは面倒ですね。このタイプの問題は3つの中ではもっとも出題頻度が低いですが、おさえておくべきコツはあります。それは、
頂点の座標のみに注目する、ということです。
放物線が動く、と考えるとものすごく大きな複雑な動きに感じられるかも知れません。ですが、頂点でしょう。平方完成すれば、すぐに求まりますからね。よって、頂点に注目すれば、以下のように簡単に解けてしまうのです。






戦略03 2次関数をマスターしておかないと……。
赤神先生が最初に言っていた通り、2次関数は高校数学最初の壁です。ですからつまずく人も多いわけですが、最初の壁だからこそ、しっかりマスターしないといけない理由があります。
簡単に言ってしまうと、それは、
2次関数で学んだことは、今後も当たり前に、それも頻繁に出てくるから
です。
たとえば、2015年度のセンター試験数学ⅠAの第1問はこんな感じです。

これ、すべて2次関数の問題です。配点は20点で、全体の5分の1を占めます。この年に限らず、センター試験の数学ⅠAに2次関数は何らかの形で毎年必ず出題されます。

2次関数ができないとセンター試験で大量失点してしまうことは、言うまでもないですね。
さらに、今これを読んでいる皆さんが今後学んでいく高校数学の問題の一例をお見せしましょう。






一番上の問題は2次関数の応用問題の典型例ですが、下2つは他の分野の問題です(それぞれ図形と方程式、微分法の内容)。
今これらの問題が解けなくても大丈夫です。知ってもらいたいのは、分野やレベルが違っても、平方完成の仕方、放物線の描き方、最大値最小値の求め方、放物線と方程式の実数解の関係などなど、2次関数で学ぶいろいろな基本的な要素をしっかり理解していないと、太刀打ちできないものが今後どんどん出てくる、ということです。
よって、厳しいようですが、2次関数でつまずいているくらいだとこの先の高校数学の学習も苦しくなってしまうのです。


戦略04 2次関数マスターへの道―具体的な勉強法

まずは、教科書や問題集を通して、基本事項の確認、および基本問題の演習を積んでいきましょう。
演習を積んでいるうちに、戦略02で教えた2次関数の典型パターンとコツを生かせることが実感できるでしょう。詳しい教科書や問題集の使い方は、以下の記事を参考にしてください。
基本問題が終わったら、応用問題に移ります。教科書の章末問題や問題集を解いていきましょう。
2次関数の応用問題としては下のような、定義域に文字が含まれる最大最小問題や、関数に文字が含まれる最大最小問題が頻出です。これが解けるようになれば、2次関数はほぼ完成、と言っても過言ではありません。

このタイプの問題では、軸と定義域の位置関係をもとに場合分けをする、というのがポイント。
2次関数の分野に限らず、これは今後の高校数学でもよく出てくる考え方です。問題集には必ずこのタイプの問題はのっていますから、問題集の解説をよく読んで、自力で解けるようにしておきましょう。
人によって差はありますが、おそらく1度でこの問題をマスターできる人はほぼいないはず。3回は同じ問題を解き直して、しっかり習得しましょう。詳しい方法は、以下の記事を参考にしてくださいね。



まとめ
☆2次関数の問題パターンとコツ
- 2次関数の最大値と最小値を求める問題
→定義域と軸の位置関係、グラフ! - 2次関数と直線、あるいはx軸との位置関係に関する問題
→判別式・軸・端点! - 2次関数を平行移動する問題
→頂点の座標だけに注目!
☆今後の数学でも、2次関数の分野で学ぶことは頻繁に使う!2次関数ができないと、他の分野にも悪影響が出てしまうので注意!
☆2次関数は、
基本事項の確認→基本問題の演習→応用問題の演習
の3ステップ。
☆特に、定義域に文字が含まれる最大最小問題や、関数に文字が含まれる最大最小問題が応用問題として頻出!軸と定義域の位置関係にもとづいて、場合分けをしながら解こう。
もっと具体的に「このとおりに勉強すれば数学の勉強は完璧、という参考書の流れが知りたい!」という方は、ぜひSTRUXの参考書マップを活用してください!

■ 参考書マップとは? ■
STRUXの「参考書マップ」は、受験までにやるべき勉強を「順番通りに」すべて洗い出したもの。「いつまでに」「どの順番で」勉強をすればいいかがひと目で分かるので、あとはこの通りに勉強するだけ!という状態になります。
- 「どの順番で」参考書に取り組めばいいかひと目でわかる!
- 「なぜこの参考書がおすすめなのか?」「かわりに使える参考書」もすべて紹介
STRUX参考書マップ公式LINEに登録することで、いつでも無料で見ることができます!
LINEに登録して参考書マップを見る













